Introduction
The first violations of Hellenic airspace by Turkish fighter jets occurred in May 1964 and were linked to the tension that prevailed in Cyprus at the time. In April 1975, Turkey asked Greece to limit the Hellenic national airspace to six nautical miles down from ten which has been internationally declared and acknowledged. Since then, Turkey has begun to question Hellenic airspace ranging between six and ten miles. Solving the problem would involve either reducing the Hellenic airspace to six miles, which is not an option for the Greek side, or increasing the territorial waters to ten miles, an option that the Greeks failed to implement. The intermediate solution chosen, i.e. sending Hellenic Air Force fighters to intercept the corresponding Turkish ones, has led to a dead-end since then.
This paper does not aspire to offer an extensive examination of the geopolitical or strategic aspects of the Greek-Turkish conflict, simply aiming at emphasising a rather technical dimension of it. What in fact we seek to investigate is the extent to which repeated attacks against Hellenic sovereign air space, which by now have developed to be a modus vivendi, reveal a certain model of behaviour, follow a certain train of thought, or pattern of reasoning. To this end, the paper is structured as follows: Section II provides a description of the data used in the analysis, while the next section links the data earlier described to the geopolitical developments in the area. Section IV fits aggressive Turkish behaviour to a statistical model which is then used to forecast this behaviour in the future in Section V. The results and the conclusions drawn are presented in the last section of the paper.
The dataset description
The activity of the THK (Türk Hava Kuvvetleri) in the Aegean either concerns cases of both a Hellenic FIR entry without informing the Hellenic Control Authority about the identity of the incoming aircraft and cases of unauthorised use of Hellenic Air Space. Refusal of an intruding aircraft to comply with the international regulations entails the use of force or the threat of use of force by the HAF (Hellenic Air Force). In most cases, the intruding aircraft abides with regulations and leaves. There have been cases, however, in which a refusal to abide leads to engagements before the intruder is eventually compelled to leave Hellenic Air Space1. This paper tackles all the above forms of actions on the part of the THK, but placing emphasis on the persistence of the Turkish aircraft in ignoring international regulations, which eventually leads to an engagement.
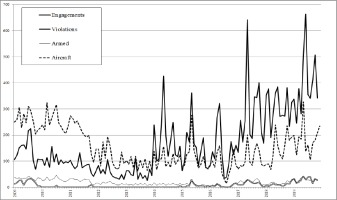
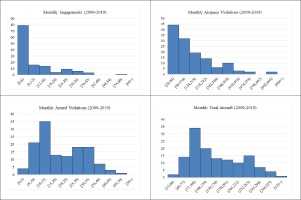
Throughout this study, we will deal with monthly datasets spanning 11 years (2009-2019) provided by the Hellenic Air Force (Hellenic Air Force General Staff, 2020). More specifically, we will consider the following categories: National Airspace Violations, Total Aircraft Involved, Armed Aircraft Violations and Engagements. Since the total number of observations for each category is 132 (11 years, 12 months), we consider 4 datasets of 132 observations in total. A graphical observation of the raw data used and an aggregate summing up is presented in Figure 1 and Table 1 respectively.
Table 1
A brief descriptive summary of the datasets (Hellenic Air Force Database, 2020)
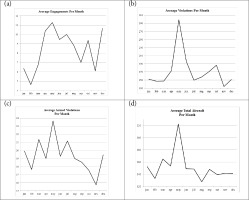
Averaging the data on a per-month basis, the following graphs (Figures 2 a, b, c, d) show a significant rise of all four categories during the second quarter (Q2) of each year. This difference can be supported using statistical hypothesis testing, but we feel that this conclusion can be readily reached just by observing the per-month graphs. The rest of the quarters (Q1, Q3 and Q4) do not follow a consistent rise/drop pattern for all categories2.
The reasoning for offensive behaviour by Turkey
The reasoning behind the prolonged pressure exercised by Turkey is threefold: firstly, demonstrating geopolitical claims in the broader Aegean area; secondly, testing the HAF speed of reaction while driving it to its limits; and thirdly, training and accustoming its pilots in what it regards as a prospective operational environment. This behaviour has not been uniform or flat. On the contrary, it has undergone significant variations, both of a short-term and a long-term character, depending on the period under consideration. Thus, since the acceptance of the Papoulia–Yilmaz memorandum terms by both the Greek and the Turkish side in 1988, friction has been avoided during the high tourist season (i.e. the summer months) as well as the major religious holidays on both sides. This explains the emphasis on the second quarter of each year which may thus be explained by the reasoning of the so called “base effect”3.
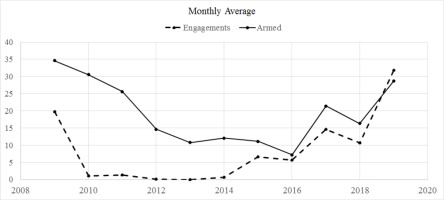
The Syrian entanglement of the Turkish armed forces between 2011 and 2015 seems to be behind the relatively “low profile” of the THK activity in the Aegean and, especially, the number of engagements which require experienced pilots. Since 2017, however, with Turkey conforming with the Russian–Syrian Agreement, a large number of experienced pilots were released to return to the Aegean front, this causing the cases and intensity of the Turkish presence in the area to rise to a considerable extent.
A great deal has been written concerning the impact of the July 2016 coup on the Turkish defence forces and, especially, on the THK. The fact is that after 2016, the pattern of the offensive behaviour against Greece has remained the same despite the military coup and the fact that in terms of intensity (proxied by engagements) it was temporarily downgraded due to the lack of experienced pilots4. During the last year of the period under study, the recovery of the THK in terms of pilot ability seems to be almost complete, with the number of engagements increasing dramatically and pushing pilots and equipment to their limits. This latest development is better described when considering that in the recent past, almost all armed THK aircraft intrusions in Hellenic air space develop into engagements (Figure 3).
In terms of geographical distribution during the period 2009-2012, the emphasis of airspace violation focused on the central Aegean with less activity observed in the north Aegean and even less in the south. By contrast, since 2013, the emphasis has shifted to the south and southeast Aegean to underline the Turkish energy claims in the area. This intense activity has been supported mainly by a fully modernised F-16 fleet to which 30 new aircraft of this type have been recently added. The activity is further supported by extensive use of Bayractar UAVs and naval air force units, while a considerable extent of force multiplication is granted thanks to seven Boeing KC-135 Stratotanker aerial refueling aircraft.
The next issue to tackle is the extent to which such extensive activity can be financed. It appears that unlike Greece, in which the overwhelming majority of the defence equipment used is imported, Turkey supports about 70% of its armed forces requirements based on domestic production, thus contributing to its GDP growth and unemployment reduction (Doulos et al., 2020). Despite the considerable involvement of the domestic defence industrial base to the armed forces procurement, the ambitious geopolitical plans of Turkey which extend from Syria to Libya, for the time being, will be rather difficult to finance given the dismal state of the Turkish economy5.
The choice of the model
In the context described above, we have already pointed out that the task which the paper faces is to consider the extent to which the THK’s offensive behaviour in the Aegean and the eastern Mediterranean follows a certain pattern of statistical behaviour. If this is the case, then we shall use this pattern to forecast airspace violations and engagements, which may be considered to represent the low – and high – intensity forms of intrusion in Hellenic air space.
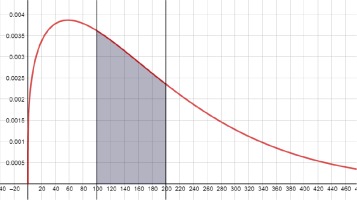
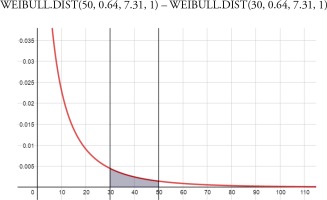
Based on the overall shape of the histograms presented in Appendix A, it is reasonable to assume that they follow a right-skewed statistical distribution. Applying the statistical method of Hypothesis Testing for goodness-of-fit, we can show that the Weibull distribution (Weibull, 1951) is an appropriate choice for interpreting both the Hellenic air space violations pattern by THK as well as the frequency of engagements and incidents between HAF and THK aircraft.
The Probability Density Function of the Weibull distribution is given by
where α, β are positive parameters. This distribution is widely used to model time-to-failure of components (Rinne, 2009; McCool, 2012). Details on the fitting method and the reasoning for selecting the Weibull distribution model for describing the Hellenic air space violations pattern, as well as the frequency of engagements incidents between HAF and THK aircraft, are given in Appendix B and C.
Forecasting the Turkish pressure in the area
Having established the model that best describes the pattern of behaviour in each of the two data categories, namely Hellenic airspace violations and engagements, we proceed with presenting our forecasting models based on the 2010-2019 period.
V.1. Logistic forecast of airspace violations with upper bound
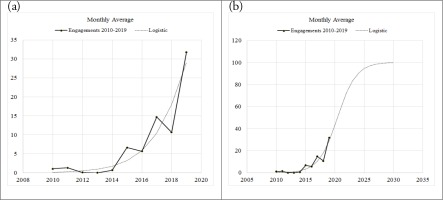
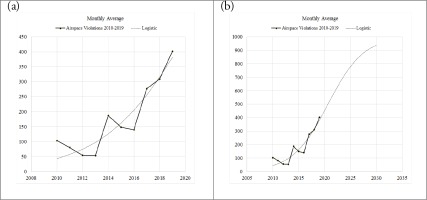
Airspace violations for the period 2010-2019 exhibit rapid growth. Linear regression could be beneficial, but we feel that it does not capture the qualitative nature of the data. Also, although an exponential model for such increase would be appropriate for the initial part, it is probably too aggressive in terms of growth.
Borrowing ideas from population growth that has been applied to a diverse set of disciplines (McKendrick et al., 1912; Edelstein-Keshet, 1988; Allen, 2007), we realise that an exponential increase of airspace violations will be, beyond a certain point, unrealistic. This is due to the fact that the Turkish side is faced with limited property and human resources (available aircraft, pilots, logistic support etc.). We consider it, therefore, more realistic to use the logistic growth, which exhibits a rapid initial rising pattern followed by a saturation based on the maximum possible airspace violations that can be expected on a monthly basis. We, therefore, resort to a logistic least-squares fit for each year to the data from 2010-2019. We calculate the squared differences of the actual minus the predicted values from the model and use Microsoft Excel’s Solver to minimise the sum by varying the parameters in the exponent. The maximum number for the monthly airspace violations assumed is 1000 used as an upper bound or “carrying capacity”, based on empirical and historical observations6.
Figure 4
Forecasting airspace violations (monthly maximum: 1000) (a) Using historical data (b) Forecasting the period until 2030
An example of the forecast works as follows: for the year 2021, the model predicts that on a monthly basis, the airspace violations will amount to an average of
We can fine-tune this forecast with the appropriate scaling for the different quarters, as we discussed earlier (in footnote 2). An example of the forecast works as follows: for the second quarter (Q2) of 2021 the model predicts that on a monthly basis, the airspace violations will amount to an average of
V.2. Logistic Forecast of Engagements with Upper Bound
We perform a similar procedure for forecasting monthly engagements, based on the logistic model, as before. Again, we calculate the squared differences of the actual minus the predicted values from the model and use Microsoft Excel’s Solver to minimise the sum by varying the parameters in the exponent setting as an upper bound 100 engagements per month7.
An example of the forecast works as follows: for the year 2021, the model predicts that on a monthly basis, if we accept the maximum 100 monthly engagements scenario, the engagements will amount to an average of
We can again fine-tune the predictions depending on which quarter we consider: For Q2 we scale with 1.09.
Discussion and conclusions
Given the above, our model concludes that the offensive behaviour of Turkey, as expressed by the pattern of Hellenic airspace violations as well as engagement incidents between HAF and THK aircraft, does not show any signs of fatigue.
In an attempt to proceed to a forecasting exercise and despite the constraints in terms of property and human resources facing the Turkish side (pilots, aircraft etc.), we have allowed for generous room for a possible increase of such attempts in the future (1000 monthly airspace violations and 100 monthly engagements). Despite such generous margins provided for our forecast, the monthly figures predicted for the year 2020 seem to be quite successful and certainly far from reaching the maximum provided for this forecasting exercise. Indeed:
(i) The model predicts that the average 2020 monthly airspace violations will be 451 with a high of 492 in the second quarter. The actual data provided thus far (June 2020) indicates that the average is 491 for the first half of the year.
(ii) The model predicts that the average 2020 monthly engagements will be 43 with a high of 47 in the second quarter. The actual data provided thus far (June 2020) indicates that the average is 45 for the first half of the year.
(iii) In terms of the forecast maximum and based on the 2009-2019 figures, we calculate that there is only a 1% probability that the number of monthly airspace violation incidents exceeds 632. Likewise, in the case of engagement incidents, a more demanding form of challenge, we calculate that there is only a 1% probability that they will be more than 80 per month.
However, these conclusions just relate to the statistical part of the problem. To proceed with a more integrated assessment, one has to take into consideration the following additional developments:
Violations of Hellenic airspace and engagements with HAF aircraft are not the only forms of pressure exercised by Turkey. Turkish aggressiveness has extended in the Aegean Sea in the form violation by Turkish ships of Hellenic territorial waters, with the latest form of pressure being the dispatch of drill-ships in the Aegean, which Turkey calls “Blue Home-land”, following similar tactics as in the case of the eastern Mediterranean. However, a primary source of threat is the massive influx of illegal emigrants from Turkey. In fact, about a year ago, the Turkish interior minister threatened that “If Turkey unblocks irregular migrant flows, no government in Europe will be able to withstand this wave for more than six months.”
The fact remains that in the recent past, Turkey has been present on a number of international fronts (Syria, Libya, Iraq etc.) However, this is a rather expensive plan for a state which is confronted with considerable economic problems8. Indeed, the Turkish economy faces an excessive current account deficit together with large amounts of private foreign-currency denominated debt and a strongly devalued domestic currency. Despite that, the authorities insist on consumption-led growth encouraged by very low interest rates, which does not seem promising in the face of such serious economic issues. With oil prices ranging at historically low levels, Qatar, practically the only ally left for Turkey, may not be able to keep on swapping Turkish liras for US dollars much longer9. This means that our forecasts on the aggressive behaviour of Turkey in the area of the Aegean and the eastern Mediterranean must be adjusted downwards to take into account the economic aspect of this issue, an aspect which points to a further downsizing as the latest data indicates.
The mathematical and statistical model presented in this paper provides a reliable guideline for forecasting and calculating probabilities of occurrences for airspace violations and engagements. However, its results require careful interpretation since our forecasts rely on the logistic model, which uses an exogenously determined fixed upper bound. More specifically, based on empirical and historical data, we impose a monthly airspace violations ceiling of 1,000 and a corresponding figure of 100 for monthly engagements. This model, therefore, is especially applicable for short- and medium-term forecasts during a time-period in which the number of available aircraft, pilots and resources is not expected to change dramatically. In light of this observation, it would be interesting to resort to further research on this technical topic involving the Hellenic sea-space violations by Turkey and the extent to which their pattern and intensity is similar to those studied herewith.